MIT-18.06|02-Elimination
消元Elimination
概述
本次 Lecture 主要讲解如何运用消元法系统化地求解
什么时候消元法有效,什么时候失效?
整门课程其实用到最多的是矩阵变换
矩阵消元具体操作
专有名词
首先这部分教授提出了一些专有名词定义
- 主元
pivot - 行列式
determinant
其中:
- 主元是我们自己定义的,如果出现系数矩阵中某一行主元为0的情况,那么我们可以在通过向下置换来实现
- 行列式=主元的乘积,这里教授只是简单引出,后续还会深入讲解
具体流程


同时我们最终可以得到原来系数矩阵A通过消元得到的上三角矩阵U(Upper Triangular)
其中方框中标出的就是我们的主元,主元是我们自己定义的,如果出现系数矩阵中某一行主元为0的情况,那么我们可以在通过向下置换来实现
消元失效的情况
正如上面所说,当想要消元得出主元的时候发现主元也消掉,出现主元为0的情况,我们就可以通过向下交换
当然如果下面没有了,出现最后一行主元为0的情况,此时消元就失效了,方程无解
换句话说,n*n的矩阵中如果主元个数最终通过置换还是不为n,那么此时消元就失效了
增广矩阵回代
教授这里将右边的b在初次消元时不带入,最终以Argument Matrix的形式接入,但是实际上还是需要遵循因消元而产生的倍增倍缩情况进行计算,最终得到一个c,c对应b正如U对应A一样

求到了这里之后就可以进行最后的回代了,原来的Ax=b现在已经转化为了Ux=c
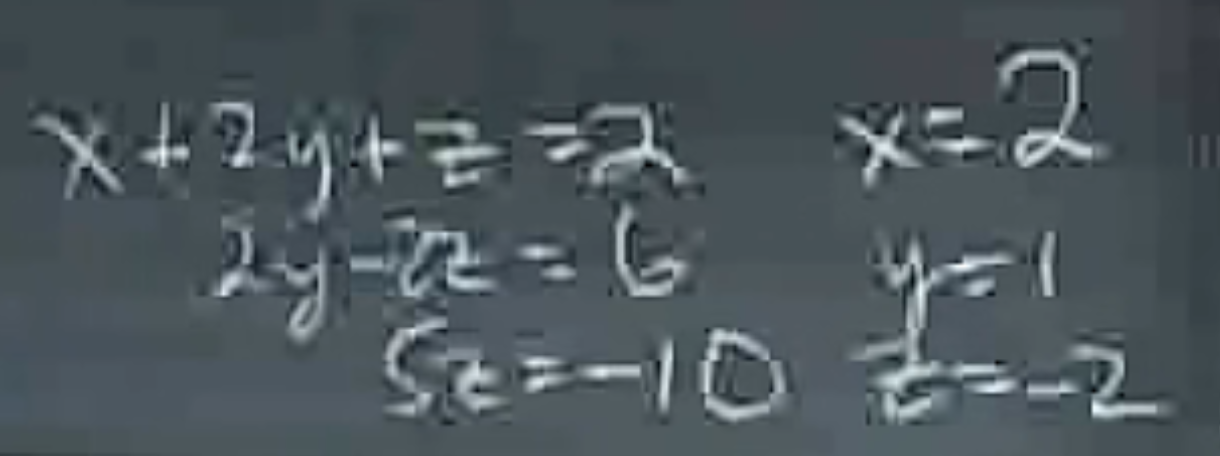
从矩阵乘法的角度来看消元
前置知识
首先教授进行了一个从线性代数本质来看矩阵操作的前置科普
主要是行和列和线性组合
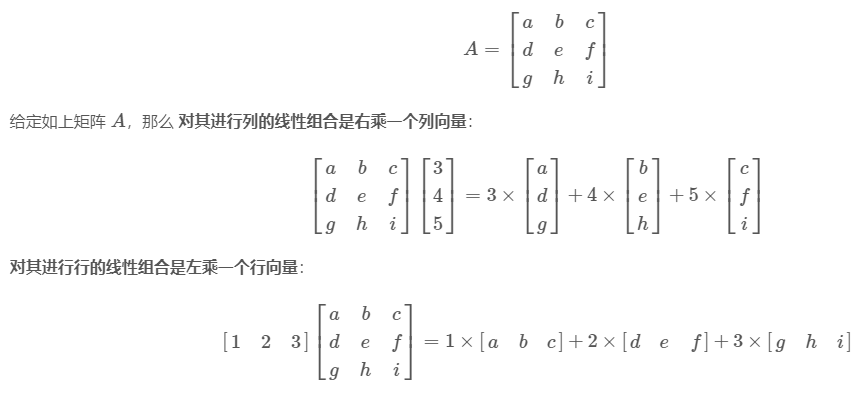
这里其实就涉及到了线性代数中核心概念:分别使用行(左乘)和列(右乘)进行矩阵操作。
矩阵乘法进行消元
在上述的基础上,教授提出了如何进行消元,可以这么理解

对于原始的系数矩阵A进行左乘操作,采用行的线性组合
[1,0,0]表示的是新结果(也就是右边)的第一行,行的线性组合应该是1倍的原来矩阵第一行+0倍的原来矩阵第二行+0倍的原来矩阵第三行
同理第三行[0,0,1]表示的是新矩阵的第三行
这也是为什么说[[1,0,0],[0,1,0],[0,0,1]]是单位矩阵,也可以从这个角度进行理解
最重要的由于我们这里需要消元的是A21,因此最终要的是第二行的操作,想要消元A21,我们就需要让-3*第一行+第二行,而不需要第三行参与,因此这里就是[-3,1,0]
总结
一个指定位置的消元不过是一次行的线性组合
从行的线性组合理解置换矩阵和逆矩阵
引入
有了上述的前置条件,其实我们就很清楚如何实现矩阵的置换以及矩阵的逆操作了
教授在最后进行整篇 Lecture 的补充
置换矩阵
不需要死记硬背,这个其实很好理解
相当于说我们让新的第一行/列是原来的第二行/列,新的第二行/列是原来的第一行/列,
行置换
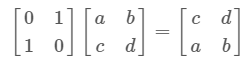
注意是左乘操作进行 行的线性组合
列置换
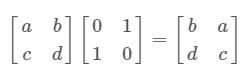
注意是右乘操作进行 列的线性组合
逆矩阵
简介
逆矩阵需要注意和转置矩阵进行区分
逆矩阵的本质其实就是为了撤销之前的行变换合并操作
如何计算
对于一个 3×3 的 矩阵 A,当我们左乘一个 E 矩阵就表示对 A 进行一次行的线性组合,是一次行变换,具体变换操作是将 −3 倍的第一行和第二行相加得到新的第二行,而第一行和第三行保持不变
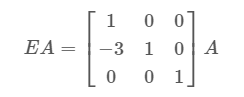
如果想要撤销其实只需要把之前加回去的给他减掉其实就行了
