MIT-18.06|01-Linear Combination

方程组的几何解释

大纲

从最经典的n个未知数n个方程开始讲起(一定有解！)

可以从三个维度进行描述

• row pic
• column pic
• matrix form

最简单的二元一次方程

这里情不自禁直接把 Matrix Form 给写出来了

row pic

核心在于针对我们的方程组，一次只取一行，作图于xy平面

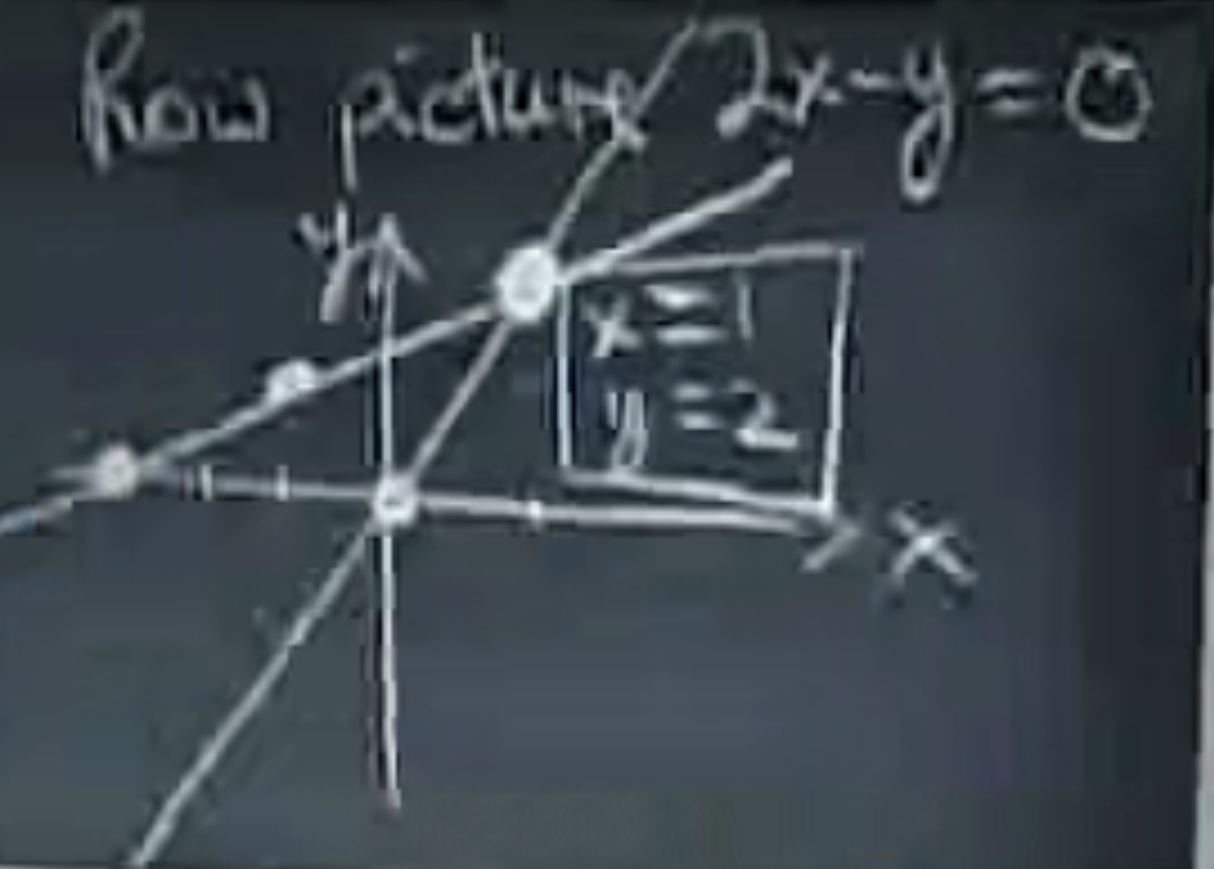
通过作图我们就可以得到，两条直线的交点就是方程组的解(1,2)(对应未知数矩阵)

column pic

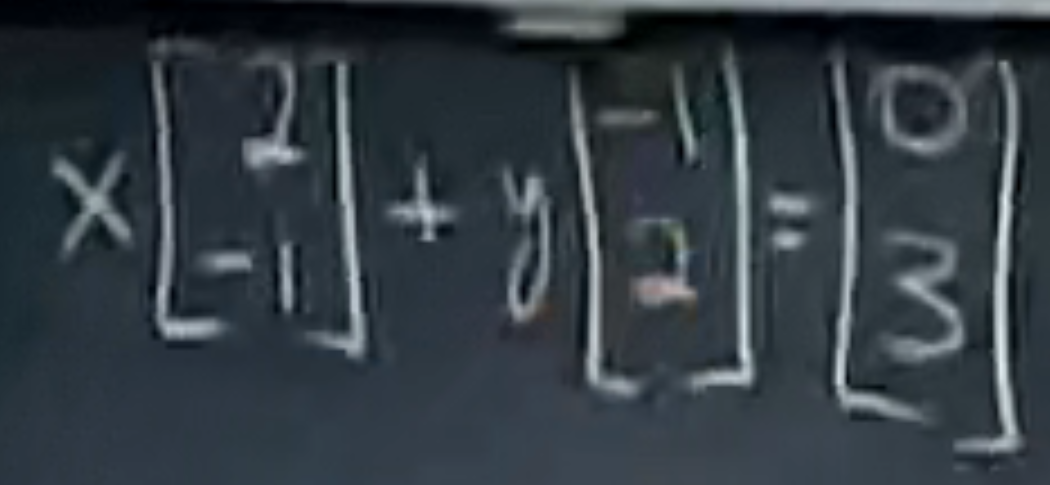
方法是一列一列获取元素，本质是通过把系数矩阵 A 进行拆分，但是右边的 b 不变

现在的问题就转换为找到一组合适的组合/解x和y，可以使得等式成立

也即 AxAx 就是对 AA 的列向量进行 xx 对应的组合（这种组合显然是线性的）

这个思想方法是后来很重要的一个线性组合(linear combination)

这里有两个列式向量[2,-1]和[-1,2]，我通过x和y以某种线性的方式来进行组合相加，这就是 linear combination

通过作图，我们可以很容易的得出结果，蓝色实线与红色实线作为不平行的二维空间基底，可以通过构造2x红色+1x蓝色来得到最终的 b 向量

延伸到三元一次方程

教授给出了一副三元一次方程

三个未知数，三个方程，一定有解！

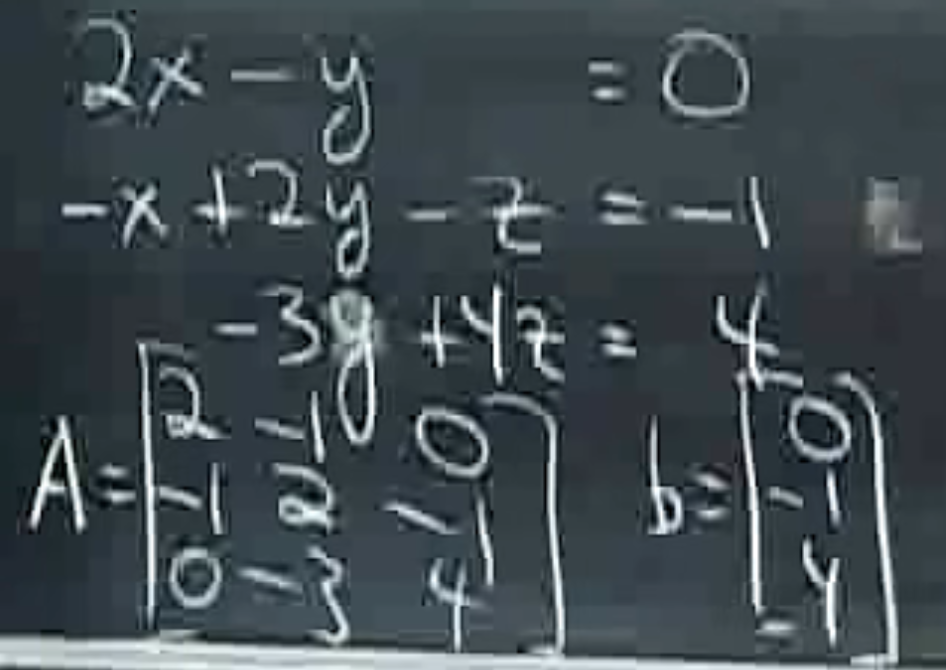
Row pic

这种方式直接进行画图其实就比较难了，由于现在是三维空间，每一行取出来都是表示一个三维空间的平面(plane)，因此画图很困难，无法直接通过每一行进行作图来画出解

不过值得明确的是，由于这三个平面一定不会平行，因此三个平面相交，一定是可以确定一个三维空间的点的，一定是有解！

Column pic

通过将系数矩阵A的列进行提取，我们可以得到下面的column pic

由于老师这里专门设计了一下，我们一眼就能看出原方程组的解为(0,0,1)，这也从侧面体现出了，采用column pic作为解决方式的快捷与直观

教授也引出了一个探讨的话题：

对于Ax=b，是不是对于任何的b都有解？

如果用线性组合(linear combination)的角度来看待这个问题，问题也可以转化为：系数矩阵中每一列的线性组合是否可以覆盖全部的空间(在这里三元是对应三维空间)

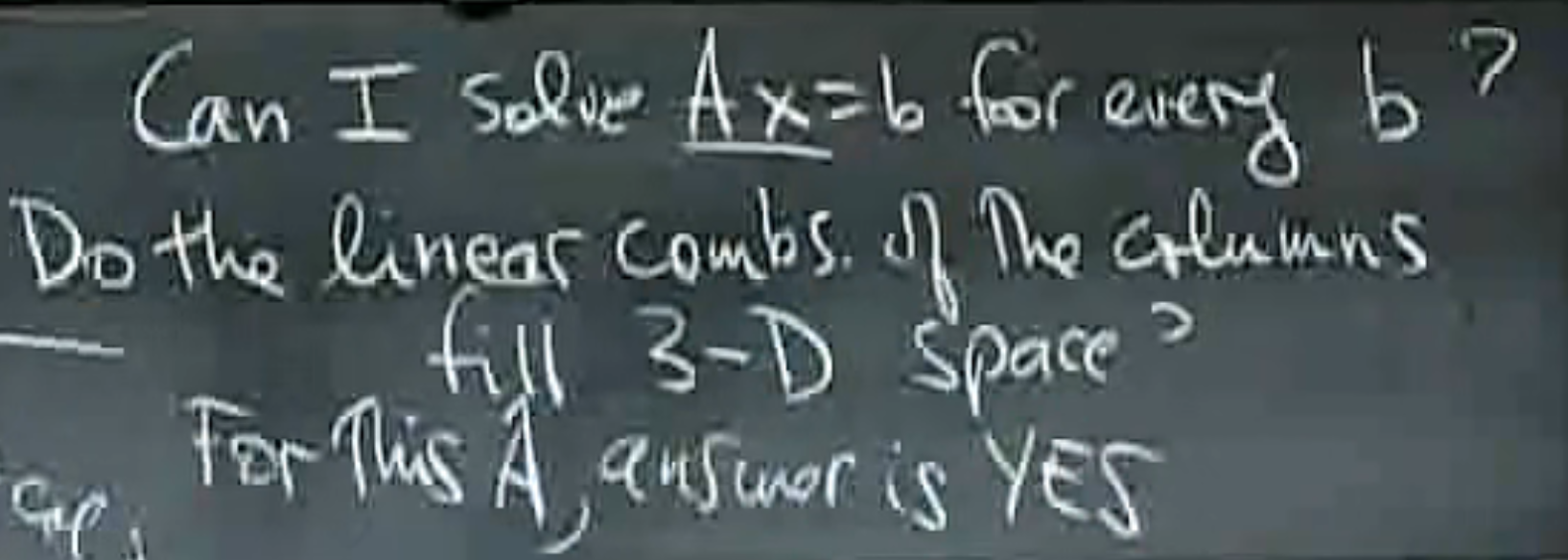
这其实是取决于我们的A的，因为在 Column pic 中，如果是三元方程组，理论上有解的 column pic 中一定是存在三个互不共面的向量来作为三个基底的，如果发现题目给的数据中存在三个向量abc，其中c可以通过ab的线性组合得来，说明他们就不共面了，因此实际上相当于你只有两个有效的方程组，三个未知数，是没有唯一解的

延申问题到九维空间

还是那个问题，对于Ax=b，是不是对于任何的b都有解？

通过迁移，其实我们也可以举一反三了，只要系数矩阵中的9个列元素都可以作为九维空间的基底（不存在说其中的某一个可以被剩下八个向量表示的情况）那么我们就一定可以通过linear combination来对这九个向量组合，得到空间的任意一个向量b

矩阵的乘法

由于之前提到过矩阵的Matrix Form，因此教授还对矩阵的乘法，形如Ax=b的乘法来进行一个讲解

例题如下：

从row pic以及column pic的角度出发，其实还是有两种角度来看待

row pic的角度

row pic 的核心思想在于一次取一行，因此我们取第一行[2,5]，点乘[1,2]^T^，得到的就是2*1+5*2=12

同理下面的就是1*1+3*2=7

column pic的角度

column pic的思想在于每次取的是系数矩阵的每一列，而最核心的辅助于他的实际上是linear combination这个核心概念

我们在乘法的时候也可以运用上这个核心的思想

上述的题目就相当于是：最终的结果=1倍的[2,1]与2倍的[5,3]进行linear combination组合得来的，直接秒杀得到[12,7]

总结

教授通过上述的问题在第一节课就提出了线性代数中很重要的一个概念：linear combination

同时也引出一个很重要的问题，是不是对于Ax=b，是不是对于任何的b都有解？

为后续奇异，可逆的矩阵性质埋下伏笔

参考

部分图片来自大佬的博客：Lec01 - 方程组的几何解释